Beyin Yakan Bilgiler Öğrenmek İsteyenler için Einstein-Cartan Teorisini En Kolay Haliyle Anlatıyoruz
Einstein-Cartan Teorisi, Einstein’ın Genel Görelilik Teorisi’nin uzay-zaman geometrisine burulmayı da dahil eden bir genellemesidir. Burulma, uzayzaman manifoldunun bir özelliğidir ve içindeki geometrik objelerin bükülmesini yahut kıvrılmasını tanımlar. Einstein-Cartan Teorisi, burulmayı da dahil ederek Genel Göreliliğin birtakım sınırlamalarını ele alır ve içsel açısal momentum yahut spin varlığında kütleçekimsel etkileşimlerin daha kapsamlı bir tarifini sağlar.
Einstein-Cartan teorisinin kökenleri ile başlayalım…
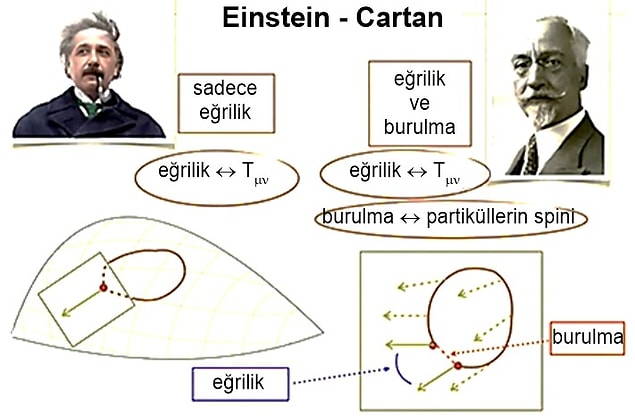
1922 yılında matematikçi Élie Cartan, Genel Görelilikte kullanılan Riemann geometrisinin doğal bir uzantısı olarak burulma kavramını ortaya attı. Sonraki yıllarda Élie Cartan, Arthur S. Eddington ve Hermann Weyl üzere bilim insanları burulmanın kütle çekim bağlamındaki tesirlerini araştırdılar. Einstein-Cartan Teorisi nihayet 1961 yılında fizikçi D. W. Sciama ve bağımsız olarak 1962 yılında matematikçi André Trautman tarafından formüle edilmiştir.
Burulma ve Einstein-Cartan-Sciama-Kibble denklemleri nelerdir?
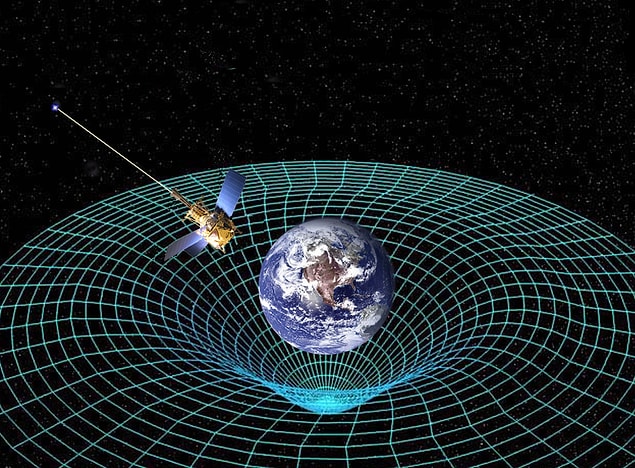
Einstein-Cartan Teorisi’nin en kıymetli özelliği, uzay-zaman geometrisinin daha eksiksiz bir halde temsil edilmesini sağlayan burulmanın dahil edilmesidir. Genel Görelilikte, uzayzamanın geometrisi metrik tensör ve Riemann tensörü tarafından verilen alakalı eğrilik ile tanımlanır. Burulmanın dahil edilmesi bu geometrik objelerin değiştirilmesini gerektirir.
Eğrilik ve burulma, Einstein-Cartan-Sciama-Kibble (ECSK) denklemlerini tanımlamak için kullanılan daha genel Cartan eğrilik tensörü tarafından yakalanır. Bu denklemler Einstein-Cartan Teorisi için alan denklemleridir ve Genel Göreliliğin yepyeni Einstein alan denklemlerinin yerini alır.

ECSK denklemleri uzayzamanın eğriliğini ve burulmasını unsurun dağılımı ve içsel açısal momentumu yahut spini ile ilişkilendirir. Spinli unsurun yokluğunda, burulma kaybolur ve ECSK denklemleri Genel Göreliliğin Einstein alan denklemlerine indirgenir.
Einstein-Cartan teorisinin kütleçekimsel etkileşimler üzerindeki tesirlerine de bir bakalım…

Einstein-Kartan Teorisine burulmanın eklenmesi, kütleçekimsel etkileşimler için birkaç kıymetli sonuca yol açar: Spin-Spin Etkileşimi: Burulmanın dahil edilmesi, Genel Görelilikte hesaba katılmayan dönen objeler ortasındaki kütleçekimsel etkileşimlerin tanımlanmasına imkan tanır.
Bu spin-spin etkileşiminin ikili sistemler üzerinde ölçülebilir tesirleri olduğu ve dönen kara deliklerin davranışında rol oynayabileceği gösterilmiştir.

Tekilliklerden kaçınma: Einstein-Cartan Teorisi, kara deliklerde yahut Büyük Patlama’da karşılaşılanlar üzere uzay-zaman tekilliklerinin burulmanın tesiri nedeniyle önleneceğini öngörür.

Sonsuz eğrilik ve güç yoğunluğu yerine, teori unsurun sonlu yoğunlukta bir duruma sıkıştırıldığını ve kozmolojideki tekillik probleminin muhtemel bir tahliline yol açtığını öngörmektedir.
Kuantum yerçekimi için muhtemel çıkarımlar nelerdir?

Uzayzaman geometrisine burulmanın dahil edilmesi, klasik ve kuantum kütleçekim teorileri ortasında bir köprü oluşturabilir. Birtakım araştırmacılar burulmanın Genel Görelilik ve kuantum mekaniğinin birleşmesinde bir rol oynayabileceğini öne sürmüşlerdir, fakat bu teorik fizik alanında açık bir soru olmaya devam etmektedir.
Deneysel testler ve müşahedeler neler, diyor?
Einstein-Cartan Teorisi, Genel Göreliliğin ilgi cazip bir uzantısını sunarken, deneysel doğrulaması devam eden bir uğraş olmaya devam etmektedir. Bugüne kadar, burulmanın varlığına dair direkt gözlemsel bir ispat rapor edilmemiştir. Bununla birlikte, birkaç dolaylı test ve müşahede, teorinin öngörüleriyle tutarlıdır.
İkili pulsar sistemleri nelerdir?

İkili pulsar sistemlerinin müşahedeleri Einstein-Cartan Teorisi için dolaylı dayanak sağlamaktadır. Bu sistemler birbirinin yörüngesinde dönen iki yüksek spinli nötron yıldızını içerir. Yörüngelerinde gözlemlenen bozulma, teori tarafından öngörülen spin-spin etkileşimi ile tutarlıdır.
Kozmolojik müşahedelere de bir bakalım…

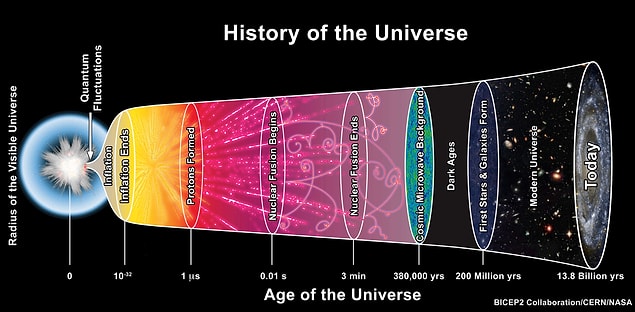
Einstein-Cartan Teorisi’nde tekilliklerden kaçınılmasının erken cihanı anlamamız üzerinde tesirleri vardır. Teoriye dayanan birtakım kozmolojik modeller, kozmosun tekrar genişlemeden evvel sonlu bir yoğunluğa kadar daraldığı bir ‘sıçrama’ senaryosu öngörmektedir.
Bu fikir, Büyük Patlama öncesi mümkün bir evreye işaret eden kozmik mikrodalga art plan radyasyonunun son gözlemlerinden bir ölçü dayanak kazanmıştır.
Kütleçekim dalgası tespiti nedir?

Kütleçekim dalgalarının LIGO ve öteki gözlemevleri tarafından tespit edilmesi, büyük kütleli objelerin kütleçekimsel etkileşimine yeni bir pencere açmaktadır. Daha fazla bilgi toplandıkça, Einstein-Cartan Teorisi’nin dönen kara deliklerin ve başka dönen objelerin davranışlarına ait öngörülerini test etmek mümkün olabilir.
Einstein-Cartan Teorisi’nin ilgi alımlı özelliklerine karşın, ele alınması gereken kimi zorluklar bulunmaktadır…

Doğrudan deneysel ispat eksikliği…

Burulma için direkt gözlemsel ispatların olmaması, Einstein-Cartan Teorisi’nin kesin olarak doğrulanmasını yahut çürütülmesini zorlaştırmaktadır. Gelecekte yapılacak deneyler ve müşahedeler, burulmanın uzay-zamanın temel bir özelliği olup olmadığını belirlemede çok kıymetli olacaktır.
Kuantum mekaniği ile uyumluluk nedir?

Einstein-Cartan Teorisi, Genel Görelilik ve kuantum mekaniğini birleştirmek için mümkün bir yol olarak önerilmiş olsa da, bu alanda yapılması gereken çok iş vardır. Dengeli ve deneysel olarak doğrulanabilir bir kuantum kütleçekim teorisi geliştirmek teorik fizikte büyük bir zorluk olmaya devam etmektedir.
Alternatif kütleçekim teorileri:

Einstein-Cartan Teorisi, yıllar boyunca öne sürülen birçok alternatif kütleçekim teorisinden yalnızca biridir. Döngü Kuantum Kütleçekimi ve Sicim Teorisi üzere öbür rakipler de Genel Göreliliğin karşılaştığı sıkıntılara mümkün tahliller sunmaktadır. Bu teorilerden hangisinin, şayet varsa, evrenimizin en hakikat tarifini sağladığını belirlemek fizikçiler için devam eden bir zorluktur.
Einstein-Cartan Teorisi, uzay-zaman geometrisine burulma tesirlerini dahil eden Genel Göreliliğin kıymetli bir uzantısını temsil eder. Bu değişiklik, bilhassa dönen objelerin varlığında, kütleçekimsel etkileşimlerin daha eksiksiz bir tarifine imkan tanır.

Burulma için direkt deneysel deliller bulmak güç olsa da, Einstein-Cartan Teorisi değerli bir ilgi uyandırmış ve teorik fizik alanındaki araştırmacılar tarafından araştırılmaya devam etmektedir.
